PISAの問題 数学編2
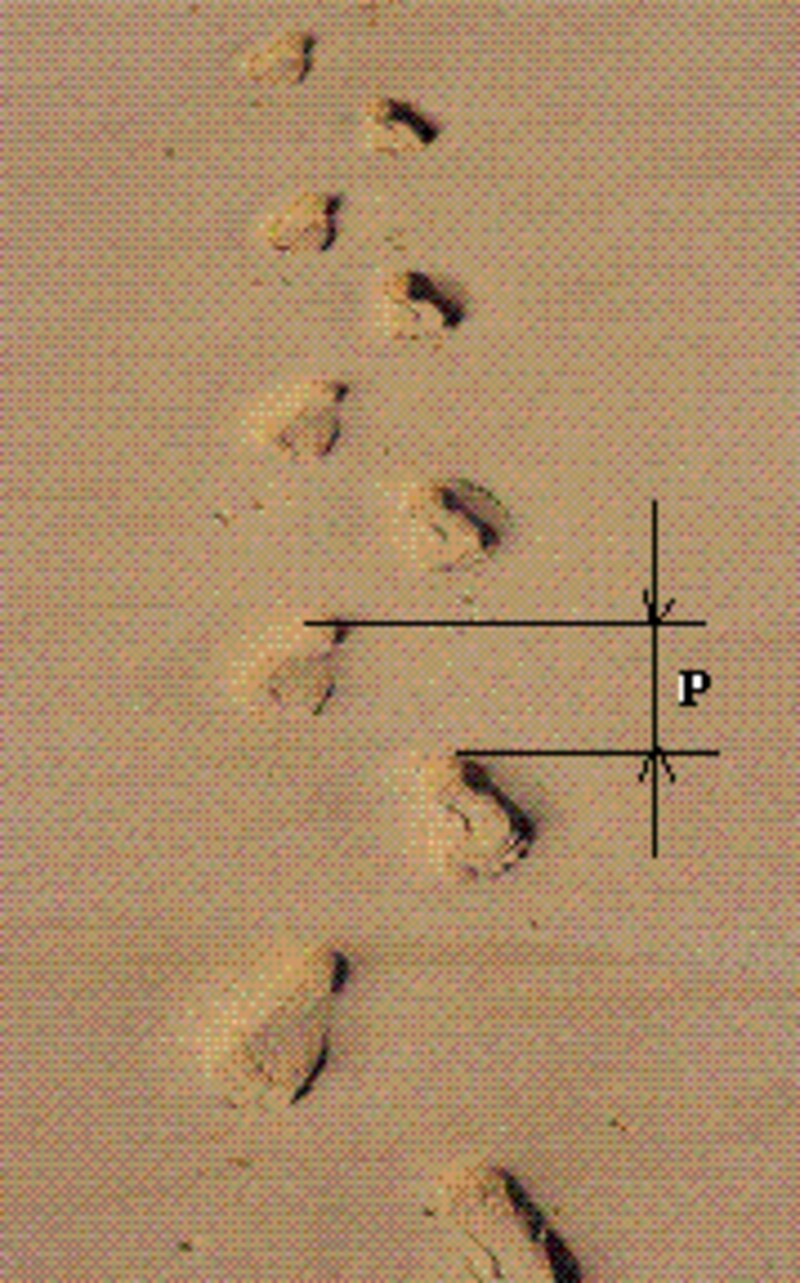
■ウォーキング問題絵は、人が歩いた足あとを示します。歩幅Pは連続する2つの足跡のかかと間の距離です。人について、公式n/P=140はnとPの近似の関係を示します。
n=毎分ステップの数
P=歩幅(m)
バーナードは、彼の歩幅が0.80メーターであることを知っています。公式はバーナードの歩きについても当てはまります。バーナードの歩く速さを毎分何メーターですか、また毎時何キロメートルですか。計算してください。
 |
問題の意味がつかめただろうか。公式が与えられているのだから、それにバーナードの速さを当てはめればいいのだが。
答え…人の歩く速さは 歩幅P×ステップ数n で表されるはずだ。バーナードの歩幅は分かっているので、毎分のステップ数nを求める。
n÷0.8=140 より n=140×0.8=112
よってバーナードの歩く速さ=112×0.8=89.6m/分 時速に直すと89.6×60÷1000=5.376km/時となる
公式は近似と書かれており有効数字が二桁なので5.4km/時と丸めてもよい。
■成長問題
1998年にオランダの青少年男女の平均身長は次のグラフのようになりました。
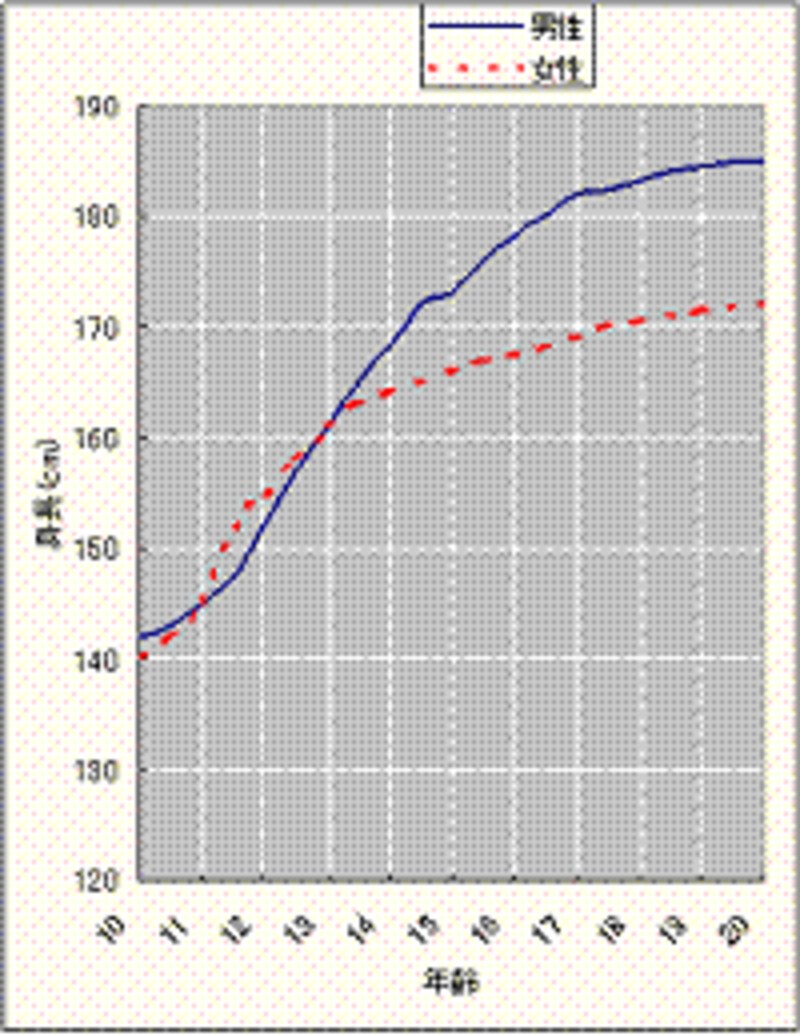 |
Q6.1980年に比べ20歳の女性の平均身長は170.6cmまで2.3cm分増加しました。20歳の女性の平均身長は1980年に何cmでしたか。
答え…170.6-2.3=168.3cm。理由:まず前提となる文に、このグラフは1998年の各年齢における平均身長と断ってある。そして1998年の20歳の女性の身長が170.6cmとあるから。
Q.7このグラフによれば、平均的に女性は生涯においてどの年齢で、同年齢の男性より背が高いですか。
答え…11歳から13歳。理由:女性の平均身長の線が男性の平均身長の線を上回っているから。
ウォーキング問題と成長問題の結果日本は8位だ。問題の意味がつかみやすかった先の問題に比べ、順位が下がっている。少々ややこしい表現のウォーキング問題と、記述で答える成長問題を苦手とする生徒がやや多かったのだろうと推測できる。
この後「為替レート問題」と「スケートボード問題」と続くが、そこで日本は12位まで順位を下げている。PISAの調査の本来の目的である「リテラシー」つまり知識を使いこなす能力を測る問題になればなるほど、日本の生徒は苦手なようだ。
「考える力」がますます問われる今後
言われているような「基礎学力でも劣る」ということはなくて(以前より下がったことは確かだが)、応用力の不足や問題文の意味を把握する読解力が不足していると考えるのが正しい理解の仕方ではないだろうか。となると単に計算ドリルや漢字書き取りの練習量を増やせば済む問題ではなさそうだ。主人公の心情読解に偏りがちな国語学習を改め、論説文や実用的な文章を論理的に理解する学習が必要だ。国語に限らず理科や社会でも知識の記憶ではなく、「なぜ?」を問う姿勢が求められている。
この点私立中学入試問題や公立一貫校の適性検査問題は、PISA調査の問題を上回る設問が多く含まれていて、「考える力」を要求するものだ。それは学校が欲しい生徒像を示しており、まさに時代が必要としている人材をこれらの学校が送り出そうとしていると考えられる。中高一貫校進学の意味がPISA調査から見えてくる。







