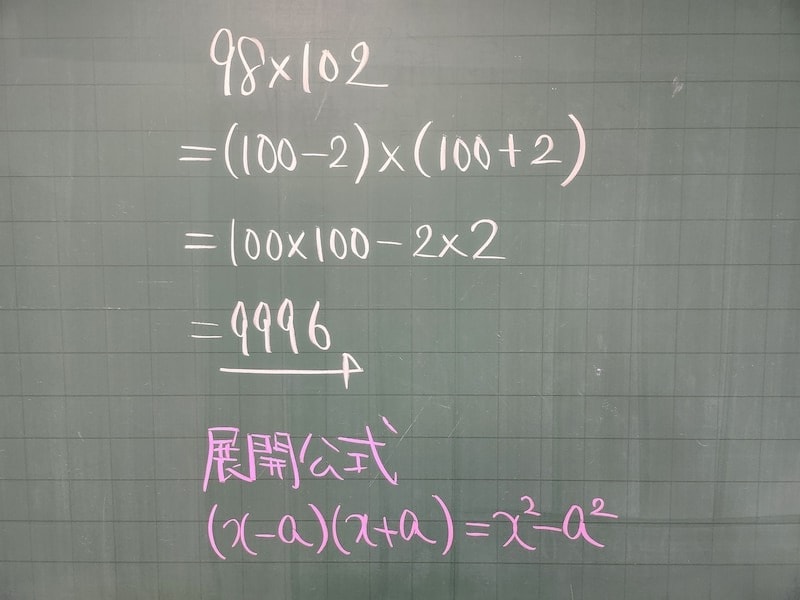葉っぱ型の面積は「半径×半径×0.57」で解けるけど… 塾で教わってくる“裏ワザ“という名の悪魔！

「図の色のついた葉っぱ（レンズ）形の部分の面積を求めよ」このような問題を解くとき、お子さんはどのようなやり方をしているでしょう。図形を斜めに分割し、4分の1のおうぎ形から直角三角形の面積を引いて、出た答えを2倍していますか。

10×10×3.14÷4＝78.5
10×10÷2＝50
78.5－50＝28.5
28.5×2＝57平方cm

多くの受験生は、このように計算していると思います。

しかし、なかには、次のように計算する生徒もいるのではないでしょうか。

10×10×0.57＝57平方cm
 

裏ワザの罪

なぜこの式で回答が出るのかと問われると、彼らは「だって塾の先生にそう習ったから」と答えるでしょう。図の葉っぱのような形の面積を「半径×半径×0.57」と教える塾講師がいるのも事実です。さきに示した4本の式を使って解くよりもはるかに楽ですから、それを教わると子どもたちは、原理もわからずやみくもにその“裏ワザ”を使用して問題を解きます。

この裏ワザの罪はふたつあります。まずひとつ目は、応用がきかないということです。裏ワザが使える問題はごく限られています。全く同じタイプの問題が出題されれば使えるでしょうが、ちょっとひねられたり、切り口を変えられてしまうと、とたんに使えなくなってしまうのです。

もうひとつの罪については、実体験していただきましょう。

最初に示した問題について、葉っぱ型の面積を「半径×半径×0.57」とする裏ワザを使って解いてみてください。ただし円周率は「7分の22」とします。

実は近年、円周率を3.14以外で計算させる問題は増えてきています。学校の教科書における円周率の記載自体が以前とは変わっていることも要因のひとつですが、海外では円周率を「7分の22」として教えている国も多く存在していますし、計算力ではなく図形問題に関する理解力を問いたいのであれば、むしろ円周率の近似値として7分の22を用いて解かせる方が有効であるとの考え方もあります。

問題自体が多様化している現代において、安直に裏ワザに頼るのは危険なことといえるでしょう。そもそも原理を理解するのだってそんなに難しいわけではないわけですし、逆にそのような簡単な原理すら理解できないのであれば、私立中学に進学しても落ちこぼれてしまうだけかもしれません。
 

「98×102を1分で解く方法」は本当に使えるのか？

最近、SNSやYouTubeで「98×102を1分で解く方法」のような話題がバズっていますね。これって、本当に使える裏ワザなのでしょうか。ちょっと考えてみましょう。

まず、この裏ワザについて簡単にご説明します。「98×102」を計算するときは、一般的に筆算を使用しますよね。しかし裏ワザを使えば、1分どころか5秒で解けます。原理は簡単です。

まず、98＝100－2、102＝100＋2と考えます。すると98×102＝（100－2）×（100＋2）となります。ここで中学生時代に習った「因数分解」を思い出してください。その中に、もっとも覚えやすかった公式がありましたよね。

そう、「（x－a）（x＋a）＝xの2乗－aの2乗」というあれです！ それに当てはめると、（100－2）×（100＋2）＝100の2乗－2の2乗＝9996になるというわけです。非常に簡単に解けるため、「これならもう筆算で計算する必要なんてないじゃん！」と数多くの人が思い、バズるわけです。

でもちょっと待ってください。ではお聞きしますが、「92×107」とかだったらどうするのですか？ この因数分解の裏ワザが使えるのは、100をはさんで前後同じの大きい数と小さい数のかけ算の場合だけですよね。この場合、92＝100－8 、107＝100＋7となるように、数字が違えばとたんに使えなくなってしまいます。

また「74×126」のように、前後で同じ数だけ離れているような数の場合でも、74×126＝（100－26）×（100＋26）＝100の2乗－26の2乗となって、26の2乗が暗算でできなければ、結局その部分で筆算を使うことになり、かえって時間がかかってしまうのではないでしょうか。こうなるともう、どのあたりが裏ワザなのかわからなくなってしまいます。
 

インド式がすたれたわけ

今から10年ほど前に「インド式」なる計算方法が世の中を席巻し、ネットでもかなりの盛り上がりを見せ、書籍も何冊も出版されました。

空前のインド式ブームが起こりましたが、その後、学校教育や塾の授業で採用されたという話は全く聞かず、2年もするとブームは去って、だれも話題にしなくなりました。

ところが、昨年あたりから同じような計算方法が、SNS上で再度ブームを巻き起こしているようです。要するにあれですね。「これって、実は全然使えなくない？」と皆が気づいてブームはいったん去ったものの、それを知らない次の世代が再び騒ぎ出している、こんな感じでしょう。

時期がくれば、またその実態に気づきブームが去る。そんな流れです。
 

学習にうまい儲け話などない

筋トレを例に挙げるとわかりやすいのではないでしょうか。たしかに、効率よく筋肉をつけようと思ったら、やみくもに筋トレするのは無駄が多いものです。自分が筋肉をつけたいパーツに集中して負荷を与えることで、効率よく鍛えることができます。すなわち、コツというものが存在します。しかし負荷をかけなければ、筋肉をつけることはできません。コツはあっても、負荷をかけなくていいという話にはならないのです。

もしあなたが「つらいトレーニングなど一切不要で、りっぱな筋肉をつけられます！」という宣伝広告を見たら、誇大広告もしくは詐欺ではないかと感じるのではないでしょうか。そんなうまい話は、この世には存在しないのです。存在するのならとっくに世界中に広がっているでしょうし、世界中の人たちは全員筋肉ムキムキになっていることでしょう。

学習だって同じことです。楽に頭が良くなる方法なんてあるはずがないのです。もちろん勉強にもコツはあります。でも、そのコツは「効率よく学力を伸ばす勉強法（負荷のかけ方）」であって、「この裏ワザを使えば頭が良くなる」というものではありません。むしろその裏ワザに頼ることにより、“学習の本質を見失ってしまう恐れ”すらあります。

うまい儲け話には、十分注意しましょうね。