「はじき」の公式を使うと、難しい速さの問題が魔法のように簡単に解けるということで、子どもたちには人気です。ところが塾講師の間では、「はじき」ほど最凶・最悪と呼ばれる悪名高い公式はありません。いったい何が問題なのでしょうか。
速さの問題が簡単に解ける「はじき」の公式とは？
まずは「はじき」の公式を知らない人のために、ひと通り説明しておきましょう。「はじき」とは、“はやさ・じかん・きょり”の頭文字をとったものです。
・は……速さ
・じ……時間
・き……距離（道のり）
「はじき」の公式とは、速さと時間と距離（道のり）を左下に「は」、右下に「じ」、上に「き」と表して解く公式。
そして、左右の関係はかけ算を、上下の関係はわり算（分数）を表します。例えば、速さを求めたい場合は、指で「は」の部分をかくせば、「き÷じ」を計算すればいいことがわかります。まさに、ドラえもん顔負けの便利な道具というわけです。
教科書の問題例を参考に説明していきましょう。
（1）速さを求める問題
ある自動車は150kmを2時間で進みます。この自動車の時速を求めましょう。
（2）距離（道のり）を求める問題
時速240kmで走る新幹線があります。この新幹線が2時間走ると何km進みますか。
（3）時間を求める問題
台風が時速15kmで進んでいます。300km進むのにかかる時間はどれだけですか。
一つ目の問題は、速さを求める問題のため「150÷2」を計算すればいいのですが、では、なぜ「150×2」ではないのでしょうか。この理由を「はじき」の公式を使って説明すると、「は」をかくすことで「き÷じ」を計算すればいいからということになります。
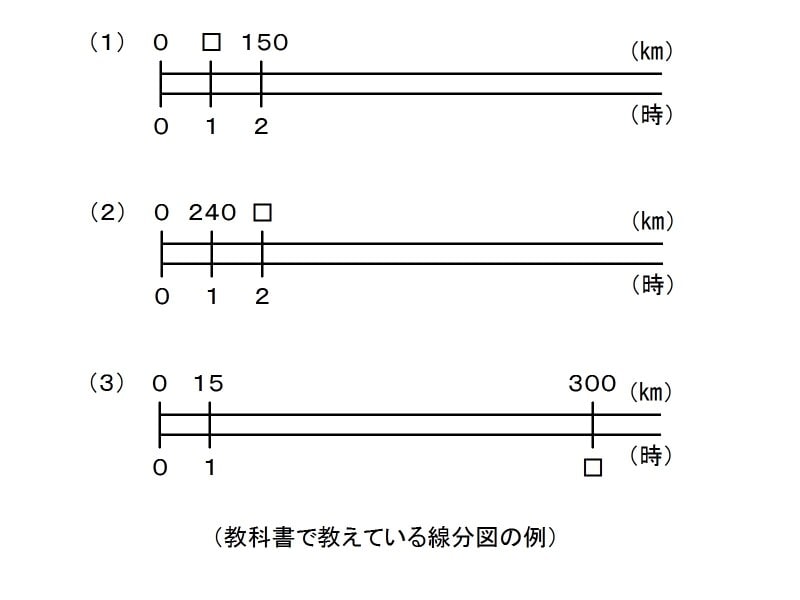
ところで小学校の算数の授業では、速さの問題をどのように教えているのでしょうか。教科書では、図のように「数直線」を使う解き方が紹介されています。実は、速さの概念の理解を難しくさせてしまう根本的な原因は、「はじき」の公式以前に、このような教え方にあります。
算数の教科書では、速さの問題は「数直線」を使って解く。この数直線と「はじき」の公式を使った教え方には、共通した決定的な問題がある。
例えば一つ目の「速さ」を求める問題なら、2にあたる数が150なので、□にあてはまる数は「150÷2」を計算すれば求められることがわかります。しかし、なぜ□がその位置にあるのかという意味までは考えないのです。
もちろん、数直線を使って教えること自体に問題があるわけではありません。しかし、最初から数直線が書かれていると、その意味も理解せずにただ図に書かれている数字を機械的に計算するだけになってしまいがちになります。これでは「はじき」の公式を使って解いているのと大差がありません。
そして事実、数直線が書かれていない問題になると、とたんに解けない子が増えるのです。つまり、数直線が書かれていたから解けただけで、速さの概念がわかっているから解けたわけではないということです。
「はじき」の公式を使うと、ますます問題文を読まなくなる
「はじき」の公式はもちろん、数直線を使わないと速さの問題が解けない子は、次のような問題で確実にひっかかります。＜問題例＞
太郎君は時速6kmの速さで走っています。30分間に何km進むでしょう。
このような問題になると「はじき」の公式で味を占めている子は、「き」を求めるには「は×じ」を計算すればいいと安易に考えて「6×30＝180km」と答えてしまいます。人間が走って30分間で180kmも進むことは不可能です。数直線が書かれていないと解けない子も同様です。中にはあろうことか「30÷6＝5km」と計算してしまう子もいます。
このような誤答をする根本的な原因は、問題文を読んでいない（特に単位を見ていない）ことにあります。6と30という2つの数字を「かける」か「わる」かをすれば解けると思っているのです。
「はじき」の公式を使って解く子はもちろん、数直線を使って解く子も、そもそも速さの問題以前に、問題文を読んでいないことがつまずきの原因ということがわかります。
数字を“つまみ読み”しただけで、文章題を読解した気になっている
文章題なのに問題文を読んでいないというこのような根本的な問題を解決するためには、正しく読むという思考スキルを身に付けるほかありません。そのためには、書かれている内容をイメージして理解できるように、子どもがわかりやすい言葉で言いかえる必要があります。冒頭で紹介した教科書の例題の一つ目の「速さ」を求める問題では、時速とは「1時間あたりに進む距離（道のり）」と言いかえます。そうすると2時間で150km進むということは、1時間で何km進むかを考えればいいわけですが、それでもわからない場合は「2つ分で150kmなら、1つ分は何kmか」と言いかえてもいいでしょう。
二つ目の「距離」を求める問題では、「時速240kmで走る」を「1時間で240km進む」と言いかえます。そして2時間なら2倍の「240×2＝480km」、3時間なら3倍の「240×3＝720km」と考えます。だから速さと時間は距離と比例の関係になることがわかります。
三つ目の「時間」を求める問題の「時速15kmで300km進むのにかかる時間」は、少し難しくなります。これはわり算の中でも「包含除（ほうがんじょ）」といって、〇の中に□がいくつあるかを考える計算だからです。
このような問題でもまずは、時速15kmを「1時間で15km進む」と考えます。次に、表し方を逆にして、「15kmで1時間」と考えるようにします。そうすると「15kmで1時間」なので「30kmなら2時間」、「45kmなら3時間」、では「300kmだと何時間になるか」を考えればいいことがわかるのです。そして「15kmにつき1時間」なので、300kmだと何時間になるかを「300の中に15がいくつあるか」と言いかえます。そうすると、「300÷15」を計算すればいいことがわかります。
それでは、先ほどの太郎君の問題はどうなるでしょうか。時速6kmとは「1時間に6km進む」と考えます。2倍の2時間なら「6×2＝12km」、3倍の3時間なら「6×3＝18km」進みます。
では、30分間で何km進むかはどうなるかというと、「6×30」では求められません。時間の単位が「時」ではなく「分」だからです。つまり「速さ×時間」を計算する前に、30分間が何時間かを考える必要があります。1時間は60分なので、30分は「30÷60＝0.5時間」となります。ここで初めて「6×0.5＝3km」と答えを求めることができるのです。
問題文を正しく読んで解いていく「読解」「思考」を育む働きかけを
このようなプロセスこそが、いわゆる「読解」や「思考」と呼ばれる過程です。「はじき」の公式や数直線は思考のツールでしかないのですが、それらに頼ってしまうとほとんどの子が問題文を読んで考えるという大切なプロセスをとばしてしまいます。問題文を読まなくても、公式にあてはめれば解けてしまうからです。こうして多くの子が、問題文を読み飛ばして数字だけを“つまみ読み”して公式に当てはめることが文章題の解き方だと勘違いしてしまうのです（専門的には「誤学習」と呼びます）。「はじき」の公式が最凶・最悪と呼ばれる理由は、このような誤った思考パターンを子どもに植え付けてしまいがちなことにあります。
正直なところ、ここまで問題点を指摘してきた筆者も、よかれと思って子どもたちに「はじき」の公式を教えていた時期がありました。しかし、そのような教え方は表面的でしかなく、子どものつまずきという問題の先送りでしかないことに気が付きました。まさにお茶を濁すような指導だったのです。
速さの単元は、「速さ」を求める問題は単位量あたりの大きさ、「距離」を求める問題は比例の関係、「時間」を求める問題は包含除と、算数・数学で欠かせない概念が盛り込まれた総仕上げの単元です。それに問題文を読むことで読解力や思考力を身に付けるという点でも、とても重要な単元であることがわかります。
家庭で子どもに速さの問題を教えるときは、安易に「はじき」の公式に頼らずに、ここで紹介した「子どもがわかる言葉で言いかえる」ということを心がけてみるといいでしょう。
