理学療法士試験 運動学の問題傾向
理学療法士として、他の医療職より最も重要な運動学。物理系の計算問題は近年、必ず出題される傾向にあるため、計算問題が苦手な人はしっかりとした対策が必要です。また、例年、筋肉の作用についての出題が多いのですが、四肢体幹の筋肉の作用に加え、手指、足部などの筋肉についてもしっかり押さえて、点数の取り漏れがないようにしたいところです。
続けて、運動学の過去問題と解説に移りますが、昨年出題の問題と計算問題を解説していきます。
続けて、運動学の過去問題と解説に移りますが、昨年出題の問題と計算問題を解説していきます。
運動学の過去問題と解答
過去問題 第52回(2017年)
立位姿勢が安定しているのはどれか。
立位姿勢が安定しているのはどれか。
- 支持基底面が狭い。
- 重心の位置が高い。
- 床と足底の接触面の摩擦抵抗が小さい。
- 上半身と下半身の重心線が一致している。
- 重心線の位置が支持基底面の中心から離れている。
この答えは【4】になります。重心線は、耳垂、肩甲骨肩峰、大転子、膝関節の前部、外果の前方を通り、この線がずれると安定性が損なわれます。その他の選択肢ですが、立位の安定性において支持基底面は広く、重心位置が支持基底面に近いほど安定します。また、重心の位置が高いと身体がぐらつきやすくなりますので、重心の位置が低いほうが安定します。
過去問題 第52回(2017年)
- 平均フィードバックは試行ごとに与える。
- 帯域幅フィードバックは何回分かをまとめて一度に与える。
- 同時フィードバックは運動課題を実行している最中に与える。
- 漸減的フィードバックは誤差が一定の幅を外れた場合に与える。
- 要約フィードバックは学習の進行に伴い頻度を減らして与える。
この答えは【3】になります。その他の解答ですが、1の平均フィードバックとは、いくつかの試行分のフィードバック平均値のみ呈示することです。2の帯域幅フィードバックとは、目標値との誤差が一定以上大きくなったときにフィードバックを行うことです。4の漸減的フィードバックは、フィードバックの頻度を徐々に減らしていくことです。5の要約フィードバックは一定回数分のフィードバックをまとめて行うことです。
過去問題 第51回(2016年)
次の歩行周期で足関節が最も底屈位になるのはどれか
- 踵接地
- 足底接地
- 立脚中期
- 爪先離地
- 遊脚中期
この問題は厚生労働省の発表では、「選択肢に正答なし」とされており、採点から除外された不適切問題となります。毎年、こういった不適切問題の扱いを受ける問題は1、2問あります。ちなみに歩行周期で足関節が最も底屈位になるのは爪先離地直後となります。この説明だと、正答は4ということになるのですが、この問題の問いは「爪先離地」という爪先が床から離れる一部の瞬間だけを選択肢にしており、爪先離地前後を含めた表現ではなかったのが正答にならなかった理由と予測されます。仮にこの選択肢が「爪先離地期」だったら、爪先離地前後の瞬間も含まれる表現の為、正答は4になったと考えられます。わずかな表現の差で正答は変わりますので、問題も選択肢もよく読む事が重要になります。
過去問題 第48回(2013年)
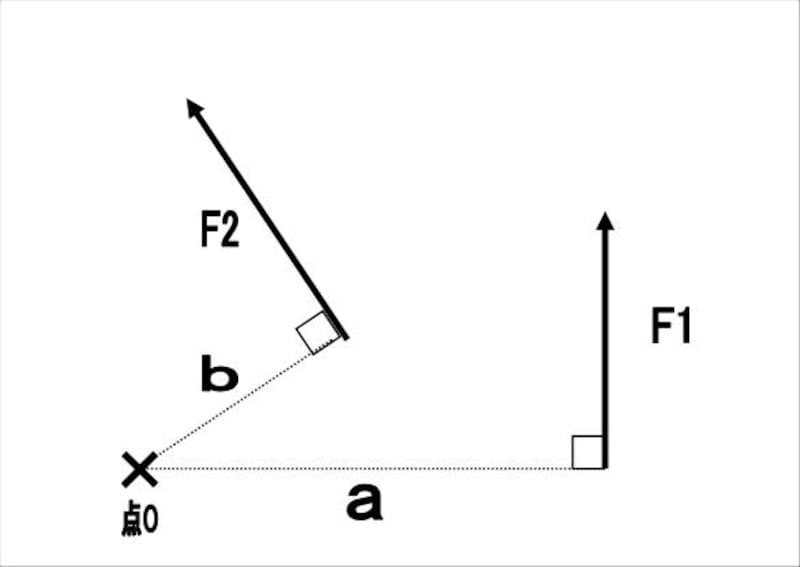
同一平面内に働く力、ベクトルF1とF2が同じ平面上の点Oの周りに作るモーメントMを表す式はどれか。ただし、OからベクトルF1とF2の作用線に下ろした垂線の長さをそれぞれa,bとする。
- M=F1+F2
- M=aF1+bF2
- M=aF1+bF2/2
- M=F1+F2/a+b
- M=(F1+F2)(a+b)
この答えは【2】となります。
この正解の2についてですが、基準点からの距離、および力の大きさの積の合計がMとなります。これについては、問題文からその問いに対する図を考えると導きやすくなり、 右に示したような図をイメージする形になります。
問題文をヒモ解いていくと、「同一平面内」とは、立体的ではなく、平面的にということ。「ベクトルF1とF2が同じ平面上の点Oの周りに作るモーメントM」とは、 点Oを軸心としてF1とF2という引っ張る力が発生した場合、引っ張る力によって生じた回転力(モーメント)をMと仮定するということになります。そして「OからベクトルF1とF2の作用線に下ろした垂線の長さをそれぞれa,bとする」というのは、点Oから伸ばした線が、ベクトル(引っ張る力)F1とF2をそれぞれ真っ直ぐ降ろした線に対し、垂直になる位置までの線。F1と垂直になる線をa。F2と垂直になる線をbとするということです。これにより、図のようなイメージ図が完成し、解答に結びつきます。文章に誤魔化されず、冷静に解いていく事が正答の鍵になりますね。
【関連記事一覧】問題文をヒモ解いていくと、「同一平面内」とは、立体的ではなく、平面的にということ。「ベクトルF1とF2が同じ平面上の点Oの周りに作るモーメントM」とは、 点Oを軸心としてF1とF2という引っ張る力が発生した場合、引っ張る力によって生じた回転力(モーメント)をMと仮定するということになります。そして「OからベクトルF1とF2の作用線に下ろした垂線の長さをそれぞれa,bとする」というのは、点Oから伸ばした線が、ベクトル(引っ張る力)F1とF2をそれぞれ真っ直ぐ降ろした線に対し、垂直になる位置までの線。F1と垂直になる線をa。F2と垂直になる線をbとするということです。これにより、図のようなイメージ図が完成し、解答に結びつきます。文章に誤魔化されず、冷静に解いていく事が正答の鍵になりますね。
理学療法士(PT)試験 総合的な問題傾向
理学療法士試験対策!手根骨(しゅこんこつ)簡単記憶法
図表化で記憶力強化!股関節の靱帯作用における勉強例