続・暗記で計算を2倍速くする方法 [小学校受験] All About

【連載】中学受験準備講座4

前回、Q.低学年の娘は算数の計算が苦手です。このままでは算数が苦手になってしまいそうですが、計算力をつける何か良い方法はありませんか？

という質問に対して「数学にも暗記」が有効という回答をしました。その後メルマガでもご紹介したとおり、講談社ブルーバックス「計算力を強くする　鍵本　聡著」を見つけ、中学受験にも応用できる内容でしたので、この本の内容をご紹介します。

同時にもっと具体例を教えて欲しいというご要望がありましたので、私が子供のために作った問題プリントの例もご紹介します。「ほんとうに2倍になるの？眉唾では？」という声も聞きますが、計算のタイプによっては2倍どころか数倍にもなります（30秒かかるものが数秒で解ける）。是非お試しください。

その前に、ちょっと下の式を見てください。これをパッと見ただけで暗算できる人は、この先を読む必要はありません。（制限時間1分30秒）

14×35＝
284×5＝
356×9＝
86×99＝
65×999＝
35678÷3の余りはいくつか？
908172635÷9の余りはいくつか？

いかがでしょうか。制限時間内にできましたか。以下の方法を使えば1分前後で上記の計算ができるようになります。

変形して楽々掛け算

算数が得意だったという人が無意識にやっていることを、計算のルールとして身に付ければ、算数が不得意な人でも計算が得意になれるはずです。それはほとんどの場合、数を分解あるいは合成して並べ替え、暗算で計算できるようにすることです。

10を探せ！分解して"2"と"5"を見つけ出し、組み合わせて10をつくり計算を簡単にする。
(例）14×35＝7×2×5×7＝49×10＝490 5倍することは10倍して2で割ること 284×5＝284×10÷2＝284÷2×10＝142×10＝1420 いかがでしょうか。ちょっと見には答えが大きくなって暗算では難しそうに思えます。でも頭の中で上記の変形をすることで、難なく暗算に持ち込むことができます。小学生の場合、無理して暗算でしなくても紙にちょっと途中の答えなりを覚書程度に書くことで、筆算を使って計算するよりずっと早く答えが出せます。また簡単な計算の組み合わせになるため、計算間違いもしにくくなります。

講談社ブルーバックス「計算力を強くする」鍵本　聡

この本は大人向けの本ですが、小中学生にも十分役に立つ内容が書かれています。著者は知っている形に持ち込んで計算する方法を「計算視力」という造語で表しています。上に紹介した方法以外にも、九九の形に持ち込んで計算視力を働かせる方法や、小数を分数に変換して計算する方法、平方や立方に持ち込む方法など多数の計算視力を紹介しています。これはお勧めです。

9が付く掛け算はちょうどの数－1

本の内容紹介ばかりではなく、オリジナルのテクニックもご紹介します。×9や×99の計算もよく入試に出てきます。筆算でやるにしても答えが大きくなって嫌ですよね。例えば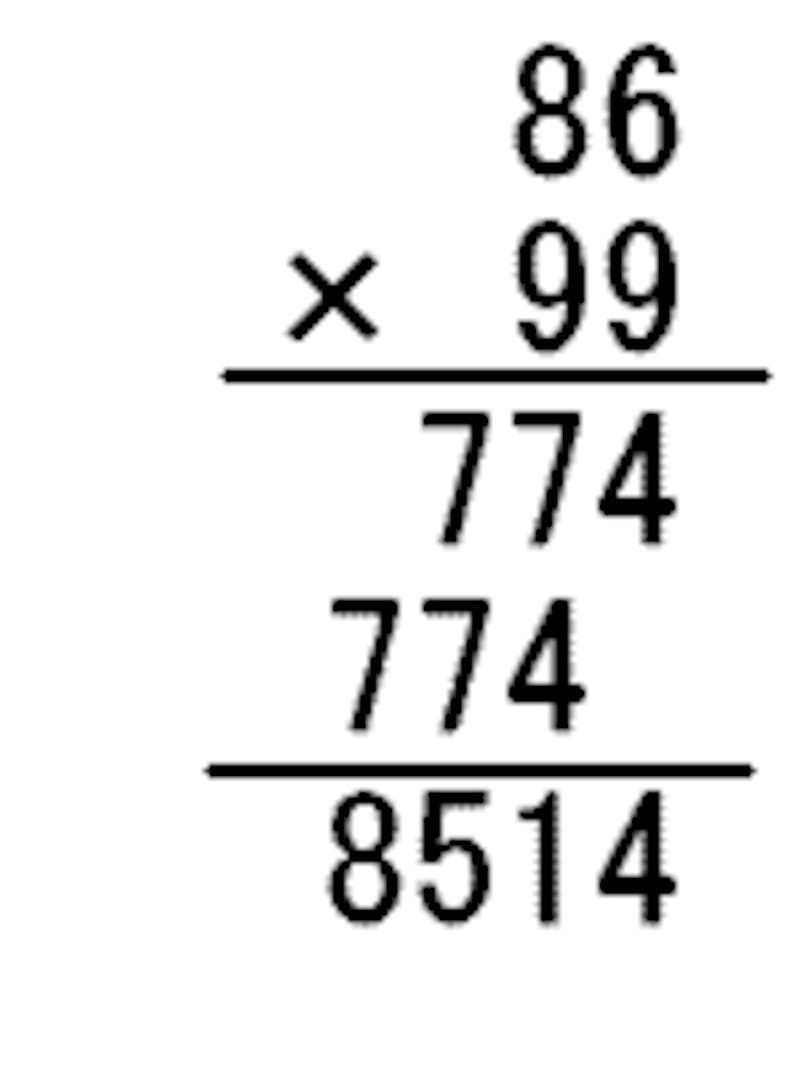

9を掛ける時は(10-1)を掛ける

のように。だから×(10-1)や×(100-1)を使います。9の桁が増えるほど効果的です。

356×9＝356×(10－1)＝3560－356＝3200＋360－356＝3204
86×99＝86×(100－1)＝8600－86＝8514
65×999＝65×(1000－1)＝65000－65＝64935

3と9で割った時の余り

整数の各桁を足した数が3または9で割り切れると、その数が3または9の倍数だということはご存知でしょう。

ところで各桁を足した数を3または9で割った時の余りが、元の数の余りになることもご存知でしたか？ 35678÷3の余りはいくつか？ 3＋5＋6＋7＋8＝29　2＋9＝11　11÷3＝3…2だから「２」 908172635÷9の余りはいくつか？ (9＋0)＋(8＋1)＋(7＋2)＋(6＋3)＋5だからこれを9で割ると5余り。だから「５」

割り算は分数にして約分してから

中学生以上であれば、割り算を分数の形に変えて計算するのが普通です。文字式ではそのように表さないといけないからです。小学生でも分数のかけ算割り算を習った後は、これを使うのは当然でしょう。

計算が不得意な子は大きな数のまま割り算していることが多く見られます。また得意な子でも、大きな数が苦にならないのでそのままにしていたりもします。しかし入試のような限られた時間の中では効率よく正しい答えを求める方が良いので、約分して小さくしてから割り算する習慣をつけたいものです。

概算する癖をつける

「計算力を強くする」の中にも概算で全体を把握するということが出てきますが、私も同感です。途中で計算間違いしたにも関わらず、とんでもない答えを書いて平気な子どもがいます。

はじめに概数でこのくらいという目安があれば、けた違いなどの間違いは気づくはずなのですが。また単位からしても、おかしいと気づくことができるセンスも欲しいですね。例えば洗濯機に入れる水の容積を求めるのに何百リットルと出てきたらおかしいと感じるなど。日常での数量のセンスを養うことも大事です。親子で意識してみてはどうでしょう。

次ページは小学生向け計算視力向上問題例