しかし、「女子だから算数が苦手」などとは言っていられない。今回取り上げるのは問題の最初に登場する計算問題だ。以前も同じ年の規則性を見つけて解く問題を取り上げた。それに比べたら計算問題なんてと思うかも知れない。しかしこれが手間のかかる計算なのだ。
問題および解説:桜蔭中学 2002年入試 算数 I(1)
 |
| 逆算の繰り返しが必要な計算問題 |
中学生であれば「移項」を利用して機械的に解くことができるが、相手は小学生である。移項と同じことではあるが「逆算」の考え方で解いていく。まずは中かっこ{}(上図の赤枠)で囲まれた部分と20/29の数の積が1であるから、{}は1÷20/29というように。
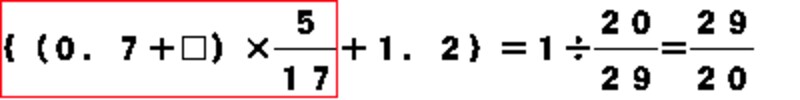 |
| 外側のかけ算を割り算に |
次は2つの数の和が分かっている時に、和から一方の数を引いて未知数(上図の赤枠)を求める逆算だ。)
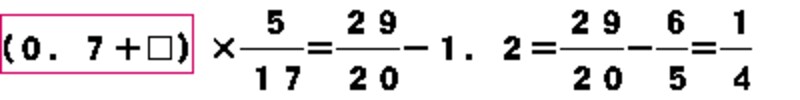 |
| 外側のたし算をひき算に |
この後も同様に逆算を続ければよい。(0.7+□)と5/17の積が求められたから、5/17で割れば(0.7+□)が求まる。
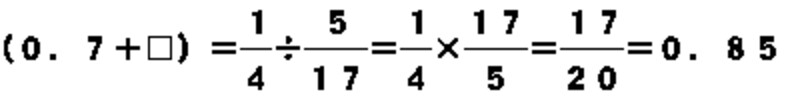 |
| 再びかけ算をわり算に |
 |
| たし算をひき算にして答えが求まる |
計算を嫌がらずあるていど機械的にこなす力も必要だ。計算量が増えてもめげずに取り組むパワーとスピードを身につけるようにしよう。
【関連リンク】
続・暗記で計算が2倍速くなる…計算力をつけるにはこれ
中学入試問題ショーケース…中学入試問題の研究にはこれ







