2005年 武蔵中学 算数よりその3 解説編
(1)はサービス問題。受験生全員ができるだろう。これは可能なお札の組合せをもれなく書き出すだけだから、頭を悩ませる必要はない。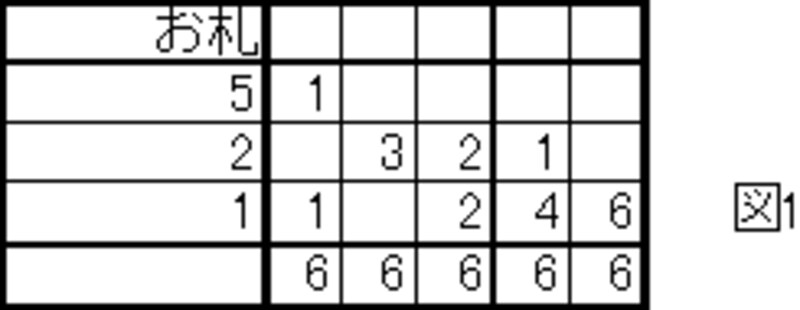
(2)は少々ややこしい。各人の証言全てに矛盾がないように組合せを埋めていかなくてはならない。
証言を考慮する前にまず9千円となる組合せを洗い出す。(1)はこれに気づかせるための配慮と考えられる。受験生に優しい問題の作りだ。

図2の8通りとなることがわかり、全員がこのどれかに該当するわけだ。これで安心して証言に取り掛かることができる。
1.A君の証言から全員の持っている金額は同じ9千円ということがわかる。
2.B君の証言から同じお札の組合せを持っている人はいないということがわかる。
3.C君の証言からC君は2千円札を持つことのできる最多の4枚持っていることが分かる(図3の黄色の部分)。
4.D君の証言からD君は、2千円札を持っていないので、5千円札1枚、千円札4枚か千円札9枚ということがわかる。
5.E君の証言の「5千円札が1枚もない」では、E君はまだ4通りの可能性があり確定できないので後に考える。
6.F君の証言からF君は最多枚数になる千円札9枚ということがわかる。従って4と合わせてD君は5千円札1枚、千円札4枚だとわかる。
ここまでをまとめると図3の通りとなる。

7.G君の証言から残りの組合せの内で枚数の差が4枚あり、多い方がA君で少ない方がG君となる。残っている組合せの枚数は3,4,6,7,8なので4枚差は3-7か4-8である。(図4)

仮にG君3枚A君7枚の組合せをここでは取ることにする。(図5)

8.H君の証言から残りの組合せの内で枚数の差が2枚の組合せは4-6と6-8の2通りある。(図4)
4-6を選ぶとH君の方が多いのだから図6となる。後回しにした5の証言との矛盾を調べると、E君は5千円札が1枚もないのだから矛盾しない。

「できたー!!」とこれで安心してはならない。答えが一通りとは限らないからだ。先ほど7で仮に置いたところで別解がないか調べることにする。G君4枚A君8枚の組合せを選ぶと、H君の証言に合う2枚差の組合せが残らないので先ほどの選択が正しいことがわかる。
では8で6-8を選ぶとどうなるだろうか。するとE君は5千円札1枚持つことになり証言と矛盾する。(図7)

以上のことから正解は図6だけである。
これは論理的思考力と、試行錯誤の労力を惜しまないねばり強さの両方を必要とする問題だと言える。このような入試問題は他の学校でも増えてきている。もし志望校でこのタイプの問題が過去に出題されていたら、パターン学習のテクニックだけを磨いても歯が立たないので、自分で考える習慣を身につけたい。特に見たこともない問題で投げ出さないことが大切なのだ。
>考える力を試す中学入試問題ショーケースにもどる。
●関連リンク
>中学受験に役立つ入試問題・勉強法リンク







