中学受験の算数は線分図と面積図をマスターせよ！　【連載】中学受験準備講座2(2ページ目)

面積図とは

同じく乱暴な言い方をすると、2元一次連立方程式を小学生が解く場合に使える方法だ。二つの量の積となる関係を表すのに都合がよい。つるかめ算や速さと距離の問題など応用範囲が広い。

（例）ツルとカメが合わせて10匹います。足の数は合計で32本です。ツルとカメはそれぞれ何匹ずつでしょうか？

典型的つるかめ算である。面積図を使わなければ、全部カメだったらと仮定して、4×10=40本の足があるはず。実際は32本なので40-32=8本。8本減ってしまったのはツルが混じっていたためで、ツルの数は8÷2=4羽。カメは10-4=6匹。と、こうなるわけだ。これを面積図に表すとどうなるか。

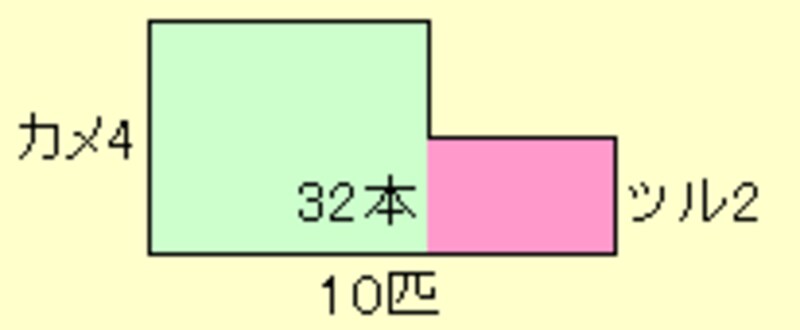つるかめ算の線分図例1

問題を素直に表すとこうなる。足の数の合計というのは1匹当たりの足の数×カメまたはツルの数の「積」で表される。そこで、ここでは縦軸に足の数を横軸に頭の数（匹数）をとる。ツルとカメでは足の数が2本と4本と異なるので段違いの図形になる。これの欠けているところを埋めて書き直してみる。

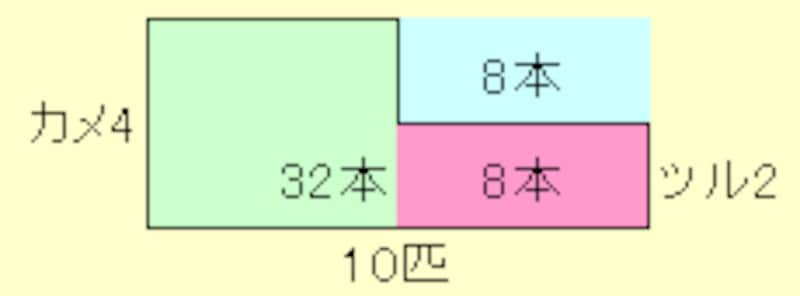つるかめ算の線分図例2

4本の足×10匹=40本で表される長方形は「全部カメだったら」である。そこで元の図形の32本を引けば、足した水色の四角で表される足の数が出る。8本である。そして図から縦軸は2本ということが明らかなので、8という長方形の面積を高さ2で割れば4という長さが出る。これがツルの数だ。

どうだろうか、こちらの方が直感的に理解しやすいのではないだろうか。全部をどちらかに仮定するという考え方は、教え込まずに使えるのは高学年の生徒だ。面積図ならば長方形の面積の求め方を習った生徒なら容易に理解できる。3年生でも使いこなせるだろう。

これら2つのツールは問題文を視覚的に表すことで、公式的な覚え方ではなく、問題文に出てくる数値の関係性を理解できるので使える知識なのだ。是非マスターして欲しい。

---

◆【連載】中学受験準備講座１ 中学受験、準備は何年生から？
◆中学受験に役立つ入試問題・勉強法リンク
中学受験に役立つ入試問題紹介やオンライン教材や出版物が購入できるページ、勉強法紹介。この中の「中学受験算数の個別指導塾・久保田塾」に詳しい線分図と面積図の解説がある。