実際のところはどうなのでしょうか。
結論をいうと、数学を学んでも身につくのは数学の知識と技能で、論理的な思考力が高まるというわけではありません。そう言い切れる根拠は3つあります。
根拠1：数学と論理的な思考力の間に、相関関係はあっても因果関係はない
よく「数学は論理的な思考力をみがくのによい教科だ」という人がいます。しかしそれは、相関関係と因果関係を混同している可能性が高い意見といえます。例えば、次のような実験があったとします。「理系の学生と文系の学生に、それぞれ同じ論理パズルを解かせてみたら、理系の学生の方が成績が良かった」というものです。実際にやってみれば、確かにこのような結果になるでしょう。しかし、理系の学生が論理パズルで高い点数をとったことからわかることは、数学の成績と論理パズルの成績との間に「正の相関がある」ということだけです。
相関関係があるからといって必ずしも因果関係までは説明できないのは、統計学を学んだ人なら知っていて当然の常識です。そう、理系に進む人は論理パズルのような問題を解く力（＝論理的な思考力）を元々もっているかもしれないからです。
一般的な感覚として「数学を学んだら論理的な思考力が身につく」ということが、実は正しくないことを示すのは簡単です。筆者の知り合いのある大学教授の言葉を借りれば、「毎日のように数学に接している数学の先生は論理的で、そうでない国語の先生は論理的ではない」と言われたら、みなさんはどう思いますか。国語の先生でなくても、だれでもこの理屈はおかしいと思うはずです。
根拠2：思考は、文脈に依存した知識（＝背景的知識）と関係がある
数学のように抽象度の高い教科を学ぶことが、必ずしも論理的な思考力につながらないことを示す実験があります。イギリスの認知心理学者であるウェイソンが行った「ウェイソンの選択課題（通称「4枚カード問題」）」と呼ばれる問題です。【ウェイソンの選択課題1：4枚カード問題】
4枚のカードがあり、それぞれの片面にはアルファベットが、もう一方の面には数字が書かれています。E、K、4、7が見えているとき、「片面が母音ならば、そのカードのもう一方の面は偶数でなければならない」というルールが成立しているかどうかを調べたいとき、最低でもどのカードをめくる必要があるでしょう。
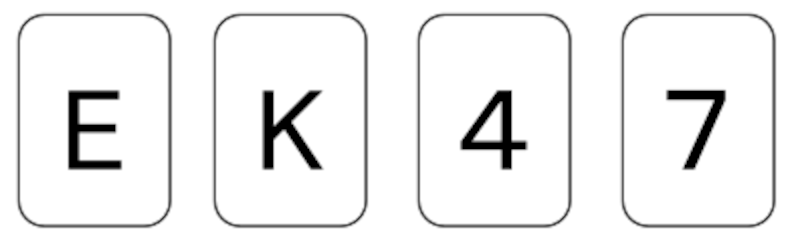
通称「4枚カード問題」とも呼ばれる、ウェイソンの選択課題1
【ウェイソンの選択課題2：飲酒カード問題】
カードの片面には年齢、もう一方の面にはその人が何を飲んでいるかという、4人の人物についての情報が書かれています。あなたは勤務中の警察官で、「もし、ある人がビールを飲んでいたら、その人は20歳以上でなければならない」というルールが守られているかどうかを調べていると想像してください。ルールが守られているかどうかを確かめるために、最低でもどのカードをめくる必要があるでしょうか。
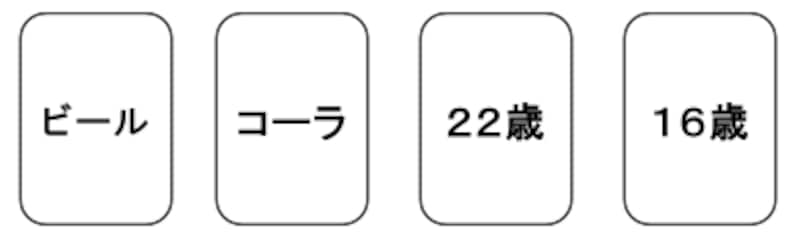
「飲酒カード問題」とも呼ばれる、ウェイソンの選択課題2
4枚カードの問題では、意外にも「4」のカードをめくる人が多いことがわかっています。これは、「片面が母音ならば、そのカードのもう一方の面は偶数でなければならない」というルールを、「片面が偶数ならば、もう一方の面は母音でなければならない」というルールと混同している人が多いためです。数学の論理命題でいえば、「逆」が成り立つと勘違いしてしまっているのです。
一方で、同じ論理構造にも関わらず、飲酒カード問題ではこのような混同が起こりません。これは、「子どもはお酒を飲んではいけないが、大人がソフトドリンク（コーラ）を飲んでも全く問題ない」という“背景的知識”が働いているからです。つまり、日常経験が判断を容易にしているためです。認知心理学ではこれを「領域固有の知識」と呼んでいます。
このことからわかることは、数学のような抽象度が高い問題を解けることと、日常的な思考力や判断力との間には、ほとんど関係がないということです。
根拠3：思考や判断の根拠になるのは、知識や経験といった情報
フリーランス外科医・大門未知子の「私、失敗しないので」という名セリフで脚光を浴びたテレビ朝日のドラマ『ドクターX』で、興味深いエピソードがあります。それは、ある高齢者に明らかに認知機能障害があり、AIが次のように診断したケースです。■AIによる診断の結果
・アルツハイマー型認知症……85％
・脳血管性認知症……7％
・パーキンソン病……5％
・その他……3％
ドラマでは認知テストも行われており、このケースはだれもがアルツハイマー型認知症と思ったことでしょう。ところが大門未知子だけが「特発性正常圧水頭症」と診断して、実際にその通りだったのです。もちろん、ドラマですから脚色はあります。しかし、大門未知子だけが他の医師とちがってその高齢者の行動を事細かに観察して、歩行障害というほかの症状があることを見逃さなかったのです。
実は、AIは診断を間違えていないことに気が付いたでしょうか。そう、「その他3％」とアルツハイマー型認知症以外の可能性をちゃんと判断しているのです。大門未知子以外は、アルツハイマー型認知症と決めてかかっていたので、AIの診断結果を読み違えてしまったのです。
もうひとつ興味深いシーンがあります。ある患者の手術中に容体が急変し、ショック状態になってしまった場面です。医学部を出た優秀なはずの大学病院の医師の誰もが原因がわからず困惑していたのに対して、大門未知子だけがその原因がわかりました。患者はゴム製品を扱う町工場を経営しており、カルテをくまなく読んでそのことを知っていた大門未知子は「ラテックス（ゴム製品）アレルギーによるアナフィラキシーショック」が起こる可能性を予測していたのです。
このように、データから思考し判断するのはあくまでも人間ですが、そもそも知識や情報を集めることから思考や判断は始まっているのです。
3つの根拠に共通していること
以上の3つの根拠に共通しているのは“背景的な知識”です。一流の棋士は、自分の対局（棋譜）をすべて覚えているそうです。といっても、素人がでたらめに配置した棋譜は覚えられません。純粋な記憶力に頼って覚えているわけではないからです。
これは野球が好きな人が、前日の試合のプロ野球12球団のスタメンを全部いえるのに似ています。野球にはポジションがあり、キャッチャーがレフトを守ったり、ピッチャーがライトを守ったりすることはありません。また打順についても、足の速い選手は一番や二番に起用されやすく、ホームランを多く打つ選手はクリーンナップを任されることがほとんどです。
実はプロフェッショナルやエキスパートと呼ばれる人たちは、その場面に関連した背景的知識をうまく活用して思考しています。
つまり思考力や判断力とは、普遍的、絶対的なものではなく、将棋や野球に関する知識の有無といった、日常的な“場面”に関する知識や経験と密接な関係があるのです。
ペーパーテストである共通テストの“最大の欠点”とは
共通テストの場合、問題にちりばめられた文章や資料の中から、必要な情報を探してきて答えを導くという点が、「思考力」や「判断力」を問う問題とされています。しかしこれらは、どちらかといえば、テキストから必要な情報を読み取る力、つまり「読解力」や「情報処理能力」でしょう。もちろん、読解力や情報処理能力が無意味というわけではありません。しかし、そのような力をトレーニングすることと日常場面で思考や判断することとが全く別問題ということは、ここまで示してきた通りです。実際に日常場面で行われる「リアルな思考」と、ペーパーテストという紙面上で行われる「バーチャルな思考」とでは、必要とされる知識も技能も異なるからです。
今後、AI社会を迎えるにあたって、データサイエンスにつながる「数学」や「情報」といった教科の学びの重要性が叫ばれています。しかし、ここまで説明してきたように「どんなデータが必要か」ということから、考えることは始まっています。
共通テストのように、始めからデータが与えられている問題をひたすら解いたところで、それは共通テストというペーパーテストの中で通用する力でしかありません。
数学の知識や技能をどう活用するかが、思考力・判断力・表現力のカギ
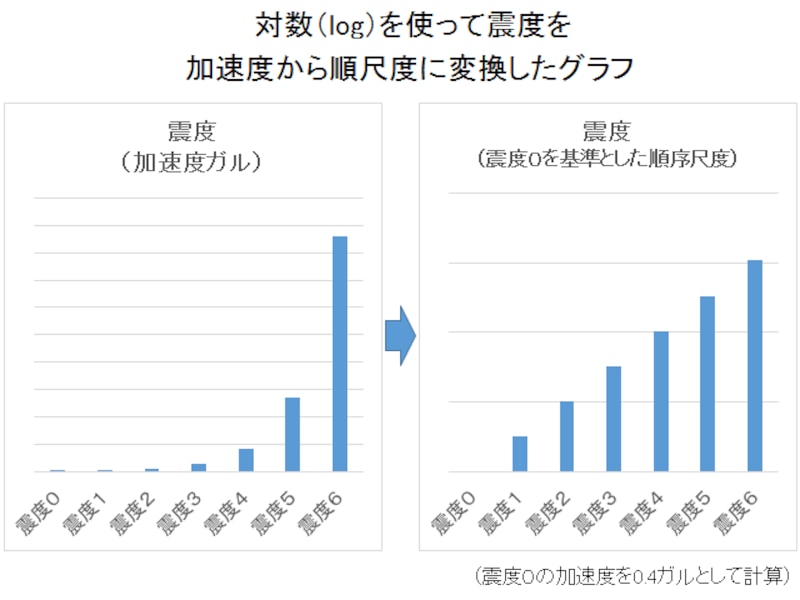
最初の話に戻りますが、数学が論理的な思考につながるとしたら、それは数学の知識や技能を日常場面で活用することにほかなりません。実際、三角関数は物理学（電気、波動など）やプログラミングなど多くの分野で活用されていますし、対数もデータを見やすく表現するために活用されています。少しだけ具体例を挙げると、地震の揺れの大きさを表す単位に「ガル（加速度）」があります。しかし、加速度だけで揺れの大きさを表すのは適切ではありません。震度が1変わると、加速度は約3.2倍もちがうからです。
そこで、対数を使って震度0～7という順序尺度で表すことで、わかりやすい表現にしています（グラフ参照。なお、グラフが見にくくなるため震度7は省略）。ちなみに対数を使って表現している例は、ほかに「地震の規模（マグニチュード）」や「星の明るさ（等級）」などがあります。
対数を使って地震の揺れを加速度から震度（順序尺度）で表現する事例
とはいえ、2023年の共通テストの数II・Bの第2問［2］（2）の「ソメイヨシノの開花予想日」の問題は、実際の活用例を用いた“良問”と考えられます。今後は、このような数学的な知識や技能を活用することにつながる問題が多く出題されることを期待したいですね。
【関連記事】
