「ミュラーリヤー錯視」は、なぜ2つの棒が違う長さに見えるのか?
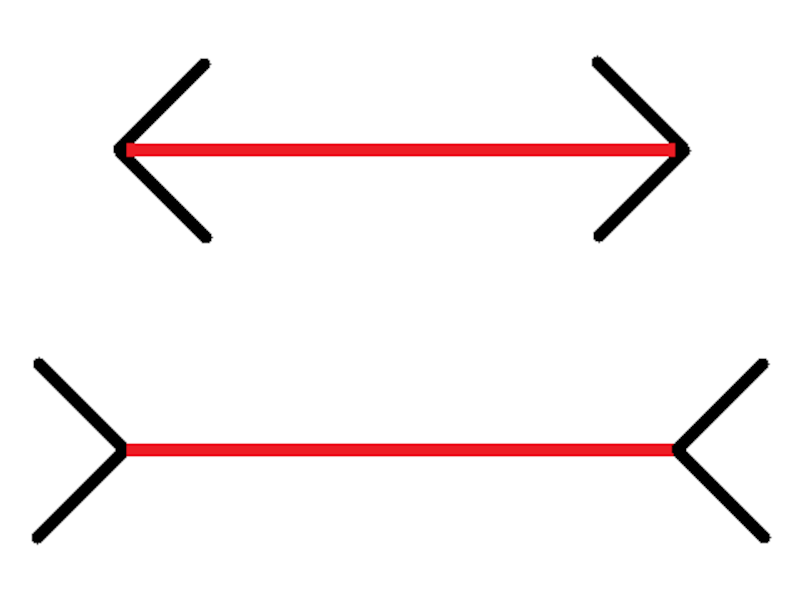
心理学の分野では、いろいろな錯視に関する図形が考案・研究されてきましたが、その中でもっとも有名なのは「ミュラーリヤー錯視」ではないでしょうか。ドイツの心理学者であるフランツ・カール・ミュラーリヤー(Franz Carl Müller-Lyer)が120年以上前に発表したもので、非常に古くから知られているので、多くの人がどこかで見たことがあると思います。下に示したのは、オリジナルを少しアレンジしたものですが、さっそく見てみてください。 オリジナルの図形はすべて黒で描かれていますが、ここでは説明しやすいように、注目してほしいところを赤色にしています。上下段に2つ図形が描いてあり、赤く示した線分の両端に内向き(上段)または外向き(下段)の矢羽がついていますね。さて、上段と下段の赤い線分の長さを比べてください。どちらが長いでしょうか。
既に答えを知っている方も多いでしょうが、実は上下段の赤い線分の長さはまったく同じです。それにもかかわらず、下段の方が長く見えませんか。知らなかったという方が「同じだ」と明かされて見直しても、やっぱり下段の方が長く思えてしまうはずです。同じ長さだと信じられない方は、両端についた矢羽を隠してみるか、ものさしを使って赤い線分の長さを測ってみてください。
この錯視はどうして起こるのでしょうか。全容は解明されていませんが、現在のところもっとも有力視されているのは、1963年にイギリス・ケンブリッジ大学のリチャード・グレゴリーが発表した解釈です。
矢羽を隠してしまうと上下段の赤い線分は同じ長さとわかるわけですから、矢羽の存在が錯覚を生じさせる要因であることは疑いようがありません。グレゴリーの説明によれば、矢羽が加わることで、私たちの脳は、この図形を「三次元的」に認識するようです。具体的には、次の図のように考えられます。
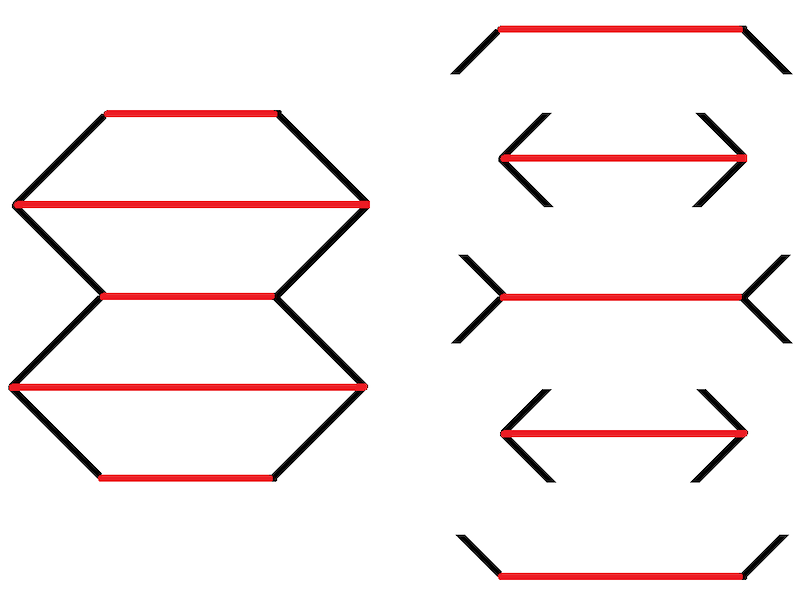
左に示したように、紙を蛇腹のように折りたたんだ状態を想像してください。両端に内向きの斜め線が入ったところの線分は、山折りになっていて手前の方にあるとみなせます。一方、両端に外向きの斜め線が入ったところの線分は、谷折りになっていて奥の方にあるとみなせます。左の図の各部分を切り離し、赤い線分の長さをそろえて描きなおしたのが右図です。私たちの脳には「遠くにある物を過大視する」という習性があるため、「今はこの大きさに見えているけど、遠くにある物なら実物の大きさは相当大きいのだろう」と考え、逆に近くにある物については「近くにあるから大きめに見えているだけで実物はそんなに大きいわけではない」と考えるのです。この習性が影響して、「同じ大きさに見える線分であっても、山折りになっていて手前の方にある線分よりも、谷折りで奥の方にある線分の方が実際には長いだろう」と脳が判断するせいで、ミュラーリヤー錯視が起こるのだと説明できます。
ミュラーリヤー錯視はシンプルですが、無意識のうちに、遠近を考慮して実物の大きさを推定しようとする、脳のしくみのすごさがわかる錯視図形なのです。