お金が2倍になるって本当？「72の法則」を資産形成に役立てよう

「72の法則」とは？資産が2倍になるまでのおおよその年数が分かる！

投資に関心のある方は、「72の法則」という言葉を聞いたことがあるかもしれません。これは、72を利回り（％）で割ると、資産が2倍になるまでのおおよその年数が分かるという、シンプルで便利な法則です。

例えば、年8％の利回りで運用できたとすると……
72÷8＝9年で資産が倍になります。 この記事では、この72の法則を活用するうえでの注意点や、背景にある「複利」の考え方について、あらためて整理してみましょう。

まず押さえておきたいのは、「72の法則は複利の世界で成り立つ」という点です。ここで、単利と複利の違いをしっかり理解しておくことが大切です。

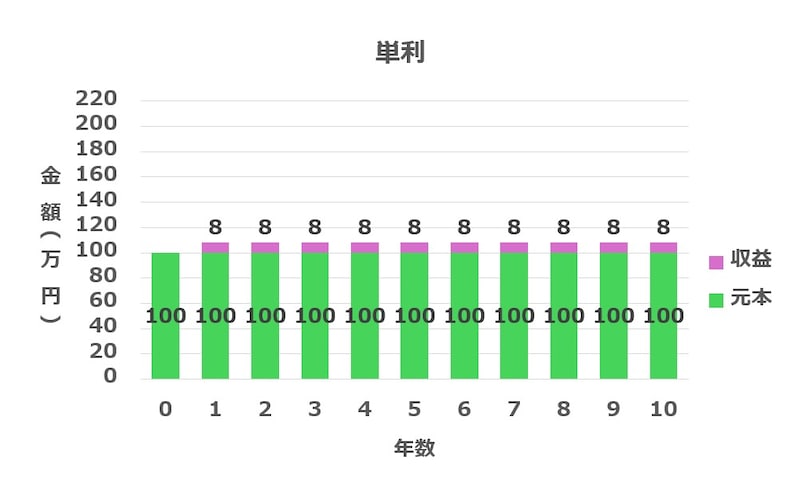
単利とは、元本（例えば100万円）にだけ毎年収益（例・定期預金の利息などを指す）があり、その収益をつど引き出してしまう仕組みです。

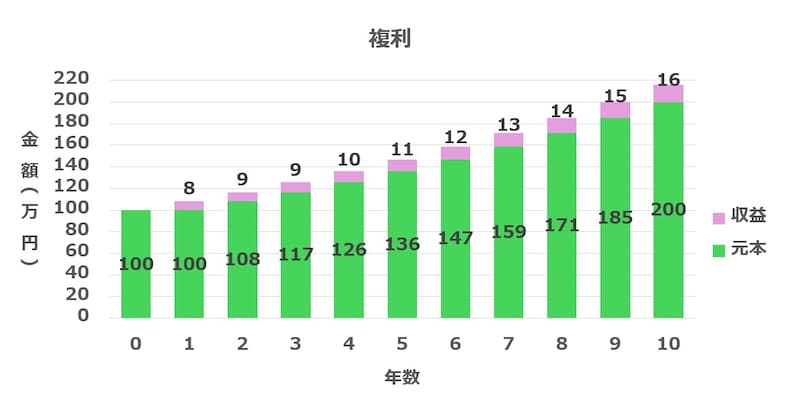
複利は、毎年得られる収益を引き出さずに元本に加え、翌年以降の運用に回していく仕組みです。収益にも収益がつくのが特徴です。

複利の威力とは？単利では12.5年かかるが、複利では9年で資産が倍になる

利回り8％のケースでは、この違いがどれほど大きな差を生むかがよく分かります。

仮に単利で年利8％の運用を行った場合、毎年の収益は8万円です。この収益を積み上げて100万円にするには、100万円÷8万円＝12.5年かかる計算になります。   ところが複利の場合、前述したように72万円÷8＝9年で2倍になります。

72万円の収益を積み上げる段階で、その収益自体も運用に回されるため、合計で100万円の収益を得るには9年で足りることになります。ここで生まれる収益の差（100万円－72万円＝28万円）が、複利の効果（威力）なのです。

この「時間を味方にする」考え方は、特に若い世代の資産形成において重要です。例えば、配当や収益を自動で再投資する無分配型の投資信託は、複利効果を最大限に生かせる商品と言えるでしょう。

さらに、iDeCoやNISAが使えない場合でも、特定口座で無分配型投信を保有すれば、本来分配金に課される税金を解約時まで繰り延べできるという税制メリットも得られます。

ちなみに、物価や賃金、経済成長率といった経済指標も、前期の水準を土台にして増えていくため、複利的に成長します。投資に限らず、「時間×成長率」の複利の考え方は、経済全体にも通じるものなのです。

投資では「72の法則」を使う場合は「複利ベースの平均利回り」で考える

ここで重要なのは、「72の法則で使う利回りは、複利の利回りでなければならない」という点です。

定期預金や国債のように金利が一定であれば問題ありませんが、株式や外貨建て資産のように利回りが毎年変動する場合には注意が必要です。

例えば、過去の運用実績をもとに72の法則を使いたい場合は、「単利ベースの平均利回り」ではなく、「複利ベースの平均利回り」を使うべきです。

なぜなら、利回りが変動する場合、単利平均は複利平均よりも必ず大きく出る傾向にあるからです。これは数学的に「相加平均≧相乗平均※」という性質に基づいています。

※「相加平均」は単に足して割った平均、「相乗平均」は複利のように掛けあわせた結果に対応する平均のことです。例えば「＋50％→－50％」という2年間の運用では、単利平均は0％でも、資産は100万円→75万円に減少します。このように、相加平均では成績がよく見えても、相乗平均（実際の複利効果）では元本割れとなるケースもあるのです。

実際の資産運用の例で見る単利と複利の違い

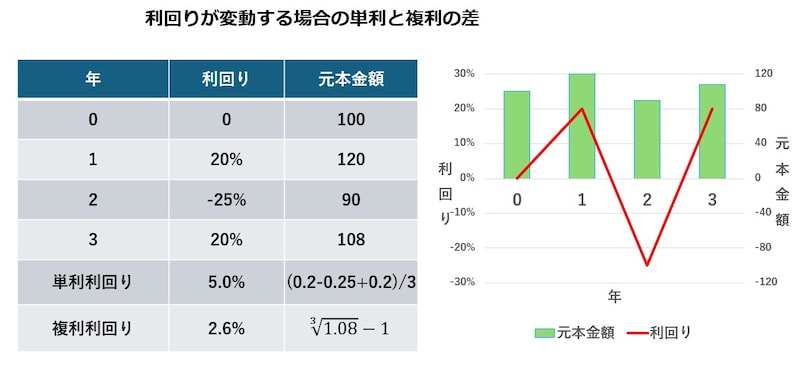
例えば、100万円を投資して、以下のように利回りが3年間で大きく変動したケースを見てみましょう。

1年目：＋20％
2年目：－25％
3年目：＋20％

この場合、単利の平均利回りは、

（20－25＋20）÷3＝5％

複利の利回りを計算するには最終元本の累乗根から1を引いて求めることとなります。エクセルの関数や、スマートフォンの関数電卓を使えば簡単に計算できます。

実際の元本は3年間で108万円にしか増えておらず、複利の利回りは2.6％程度にとどまります。   このまま72の法則を適用すると……

単利5％→72÷5＝14.4年
複利2.6％→72÷2.6＝27.7年

なんと、倍近くの差が生じてしまいます。

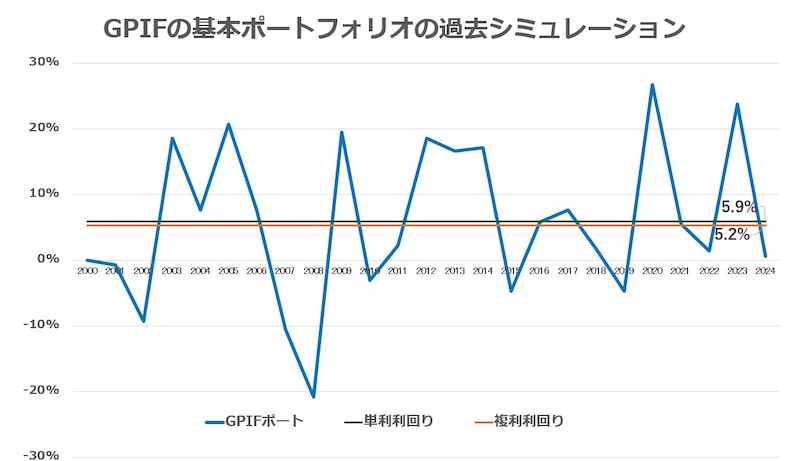
例えば、年金積立金管理運用独立行政法人（GPIF）の基本ポートフォリオで投資を行った場合、過去25年間のシミュレーションによると……

単利ベースの平均利回り：5.9％
複利ベースの利回り：5.2％

投資の場合は、「複利ベースの平均利回り」を使いますから、この複利利回りを72の法則に当てはめると、72÷5.2＝約13.8年で資産が倍になります。 ＜関連記事＞インフレにも耐性あり？GPIF（年金積立金管理運用独立行政法人）の基本ポートフォリオで運用してみよう

「72の法則」はざっくりした計算式

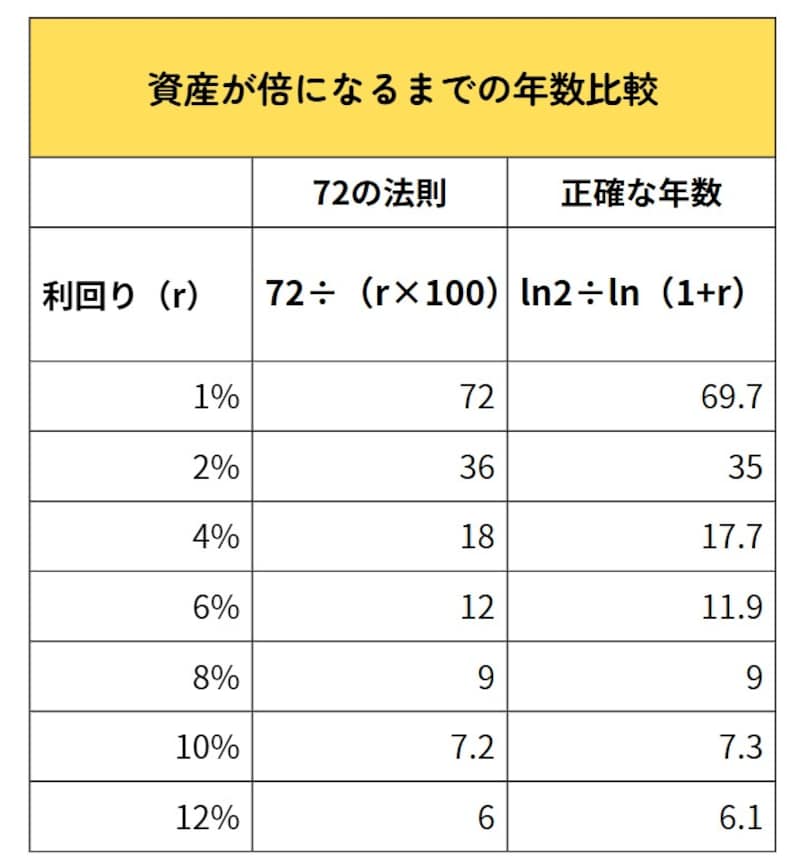
最後に補足すると、72の法則はあくまで「簡易式」です。

正確な年数は対数関数によって求められますが、72の法則はその近似値として使われます。

特に……
利回りが8％付近では比較的正確
利回りがそれより小さい場合→実際より長く出る
利回りがそれより大きい場合→実際より短く出る

という傾向があります。  
これまでのようなゼロ金利時代にはやや精度に欠ける場面もありましたが、金利上昇が進む中で、72の法則の実用性は今後さらに高まることが期待されます。

教えてくれたのは……
陣場 隆（じんば たかし）さん

京都大学法学部卒業、ペンシルベニア大学ウォートン校MBA、三井信託銀行入社、国際金融部、国際企画部、融資企画部付、年金企画部、年金資金運用研究センター出向、三井アセット信託銀行公的年金運用部次長、証券営業部次長などを経て2006年末に同社退社。2007年より年金積立金管理運用独立行政法人（GPIF）に勤務。調査室副室長、運用部長、調査数理室長を経て2020年定年退職。GPIF勤務の13年間で、運用機関構成の決定や基本ポートフォリオの策定を統括した。GPIFを定年退職後「今を生きる若い人たちに向けて年長者の知恵を伝えたい」という気持ちが強くなってきたため、執筆活動を開始